Те, що починалося як бонусне запитання на математичному конкурсі середньої школи, призвело до приголомшливих 10 нових способів довести давнє математичне правило теореми Піфагора. Довгий час стверджували, що неможливо використовувати тригонометрію, щоб довести теорему, яка фактично є фундаментальною для тригонометрії. Це впадає в логічну помилку циклічного мислення, намагаючись довести ідею самою ідеєю.

«Немає жодних тригонометричних доказів, тому що всі фундаментальні формули тригонометрії самі базуються на істинності теореми Піфагора», — писав математик Еліша Луміс у 1927 році.
Але двоє американських однокласників, Не’Кія Джексон і Кальсеа Джонсон, досягли «неможливого» під час останнього року навчання у 2023 році. Тепер вони опублікували ці результати разом із ще дев’ятьма доказами.
«Було багато разів, коли ми обоє хотіли залишити цей проект, але ми вирішили наполегливо завершити розпочате», — пишуть Джексон і Джонсон у своїй статті.
Теорема Піфагора описує співвідношення між трьома сторонами прямокутного трикутника. Воно неймовірно корисне для інженерії та будівництва та використовувалося людьми за століття до того, як рівняння було приписано Піфагору, зокрема, як стверджують деякі, під час будівництва Стоунхенджа.
Теорема є фундаментальним законом у галузі тригонометрії, який по суті обчислює співвідношення між сторонами та кутами трикутників. Ви, ймовірно, пам’ятаєте, як у школі вам втручали рівняння a2+b2 =c2.
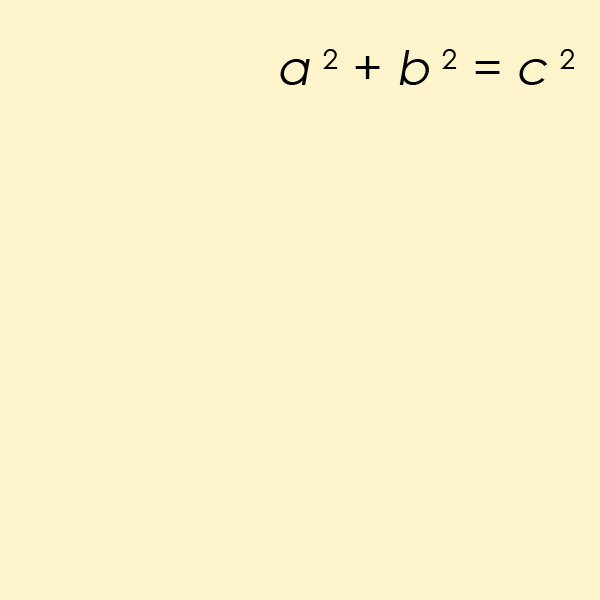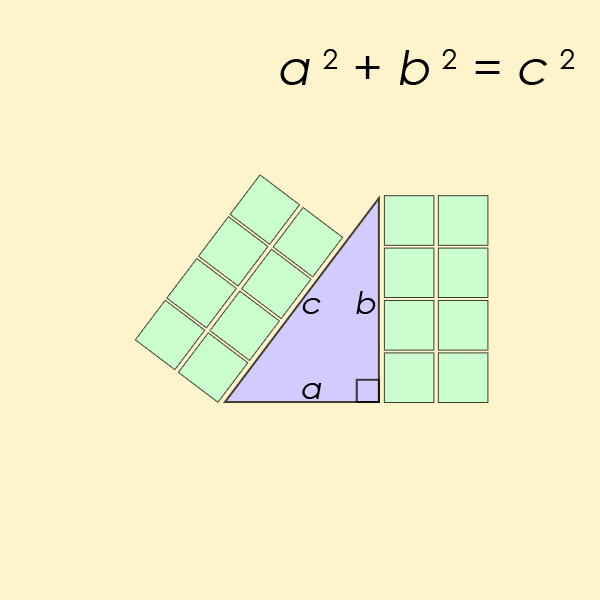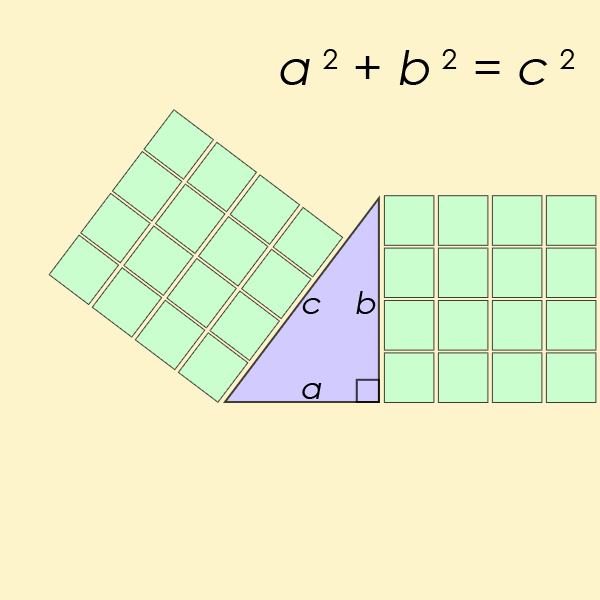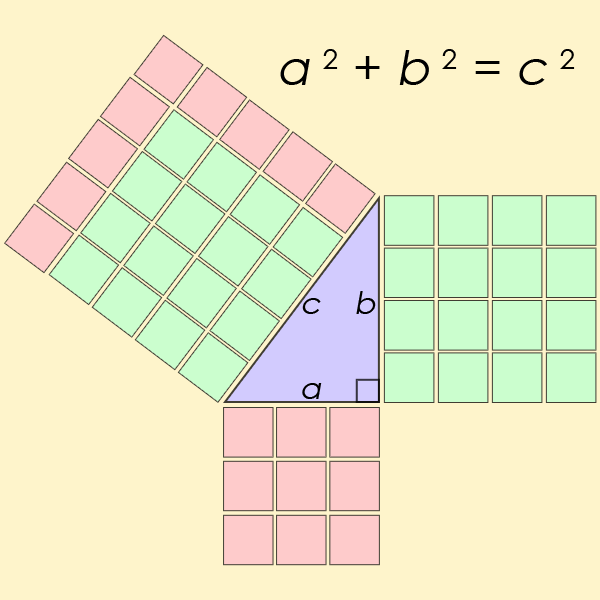
«Студенти можуть не усвідомлювати, що дві конкуруючі версії тригонометрії були вписані в одну термінологію», — пояснюють Джексон і Джонсон. «У такому випадку спроба зрозуміти тригонометрію може бути схожа на спробу зрозуміти зображення, на якому два різні зображення надруковані одне на одному».
Розділивши ці дві пов’язані, але різні варіації, Джексон і Джонсон змогли знайти нові рішення, використовуючи закон синусів, уникаючи прямого циклічного мислення.
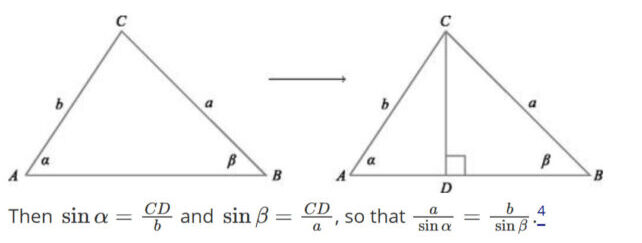
Джексон і Джонсон описують цей метод у своїй новій статті, хоча вони відзначають, що межа між тригонометричним і нетригонометричним є дещо суб’єктивною. Вони також зазначають, що за їхнім визначенням двоє інших досвідчених математиків, Дж. Зімба та Н. Лузія, довели теорему також за допомогою тригонометрії, кидаючи виклик минулим твердженням про те, що це неможливо.
В одному зі своїх доказів двоє студентів довели визначення обчислення з трикутниками до крайності, заповнивши один більший трикутник послідовністю менших трикутників і використовуючи обчислення, щоб знайти вимірювання сторін початкового трикутника.
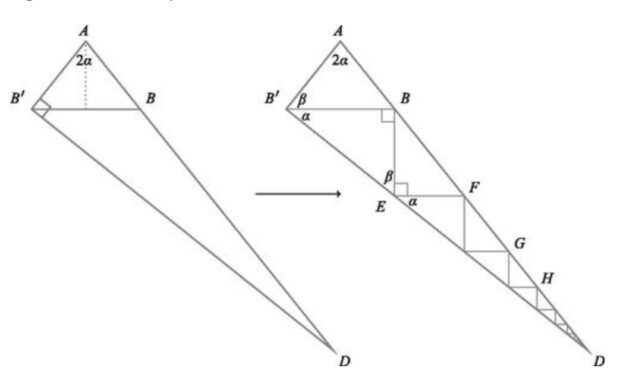
«Схоже, я нічого такого не бачив», — сказав Нікку Огасі в Science News математик Альваро Лозано-Робледо з університету Коннектикуту.
Разом Джексон і Джонсон надають один доказ для прямокутних трикутників, які мають дві рівні сторони, і ще чотири докази для прямокутних трикутників з нерівними сторонами, залишаючи принаймні ще п’ять для «зацікавленого читача».
«Опублікувати статтю в такому молодому віці – це справді карколомно», – каже Джонсон, який зараз вивчає інженерію навколишнього середовища. Зараз Джексон вивчає фармацевтику.
«Їх результати привертають увагу до обіцянки свіжого погляду студентів на поле», — каже Делла Дамбо, головний редактор журналу, у якому вони публікуються. Це дослідження було опубліковано в American Mathematical Monthly.
 245
245